연재는 매일 아침 7시에 이루어질 예정이다.
본 글은 위상수학에 전문적이라고는 할 수 없는 한낱 학생이 쓴 글에 불과하기에, 딱딱하고 엄밀하기보다는 가볍고 쉽게 풀어 쓴 글이다.
읽는 이들도 가볍게 글쓴이와 적극적으로 소통해주기를 원한다!
2장. 위상공간과 연속함수: Topological Spaces and Continuous Functions
위상공간 (topological spaces)
드디어 위상수학이라고 할 수 있는 첫 단원에 발을 내딛었다. 🤗
독자가 1장의 개념에는 이미 익숙하다고 보고, 바로 위상의 정의부터 시작하겠다. 헷갈리는 용어는 억지로 번역하지 않고 원어 그대로 실었다.
Def. A Topology on a set $X$ is a collection $\mathscr{T} \subset \mathscr{P}(X)$ having the following properties [1]
(1) $∅$ and $X$ are in $\mathscr{T}$.
(2) The union of the elements of any subcollection of $\mathscr{T}$ is in $\mathscr{T}$.
(3) The intersection of the elements of any finite subcollection of $\mathscr{T}$ is in $\mathscr{T}$ .
말이 어렵다! 그렇지만 이럴 때에는 그림으로 쉽게 이해해보도록 하자. 어느 분야의 기초적인 개념일수록 더욱 절실하게 필요한 과정이다.
아래 그림을 보시라.
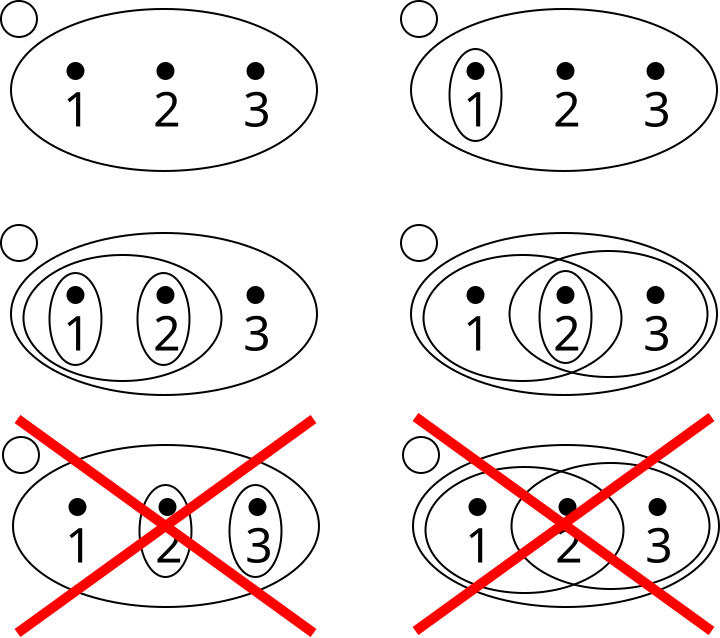
검은 점을 집합 $X$의 원소라고 하고, 타원을 $X$의 부분집합이라고 하자. 그리고 그 타원들을 모두 묶은 집합을 $\mathscr{T}$라고 하자. 각 그림의 왼쪽 위에 놓인 작은 원은 공집합을 나타낸다.
5번째 그림에서, $\mathscr{T}$는 위상이 아니다. {2}와 {3}의 합집합인 {2, 3}이 부재하기 때문이다.
6번째 그림에서, $\mathscr{T}$는 위상이 아니다. {1, 2}와 {2, 3}의 교집합인 {2}가 부재하기 때문이다.
자, 여기까지 따라왔다면 당신은 어떤 상황에서 $\mathscr{T}$가 위상이 되지 못하는지 감을 잡았을 것이다.
이제 다양한 위상의 종류를 소개하겠다.
discrete topology: $\mathscr{P}(X)$, 즉 X의 멱집합
indiscrete topology (trivial topology): X와 ∅만 원소로 가지는 위상
finite complement topology (cofinite topology, 쌍대유한위상):
$X-U$가 유한이거나 $U$가 ∅인 (이 성질을 cofiniteness라고 한다) $U \subset X$들의 집합(Collection).
대충 finer, coarser, comparable 얘기
위상의 기저 (Basis of Topology)
위상의 기저는 위상을 기술하는데 매우 편리하다.
순서 위상 (Order Topology)
곱 위상 (Product Topology)
부분공간의 위상 (Subspace Topology)
닫힌 집합과 극한점 (Closed Sets and Limit Points)
U가 x의 근방에 있다는 말을 자주 쓴다. “$U$ is a neighborhood of $x$”
하우스도르프 공간 (Hausdorff Spaces)
Def. $X$의 모든 두 원소 $x_1$, $x_2$에 대하여 각각 서로소(disjoint)인 근방 $U_1$, $U_2$이 존재하는 위상공간 $X$
연속함수 (Continuous Functions)
위상수학을 공부하기 전에, 우리는 미적분학과 해석학에서 연속함수의 정의를 계속 확장해왔다. 이제 우리는 그 정의가 가장 일반적으로 확장된 결과를 다룰 것이다. (수학은 이런 일이 너무 비일비재하다)
Def. A function $f : X \rightarrow Y$ is continuous iff. $\forall$ open subset V of Y, $f^{-1}(V)$ is an open subset of $X$
만약 $f : X \rightarrow Y$가 bijection이고, 역함수 $f^{-1} : Y \rightarrow X$가 연속이면,
이 함수 $f$를 위상동형사상(homeomorphism)이라고 부른다.
거리공간 (Metric Topology)
Def. A metric on a set $X$ is a function $d : X \times X \rightarrow \mathbb{R}$ having the following properties:
(1) $d(x, y) = 0$ iff. $x = y$
(2) $d(x, y) = d(y, x)$
(3) $d(x, y) \leq d(x, z) + d(z, y)$
Def. If $d$ is a metric on the set $X$, then the collection of all open balls in $X$ is a basis for a topology on $X$, called the metric topology induced by $d$.
몫위상 (Quotient Topology)
현대대수학에서 몫공간 (quotient space)을 공부하고 오면 이해가 쉽다.
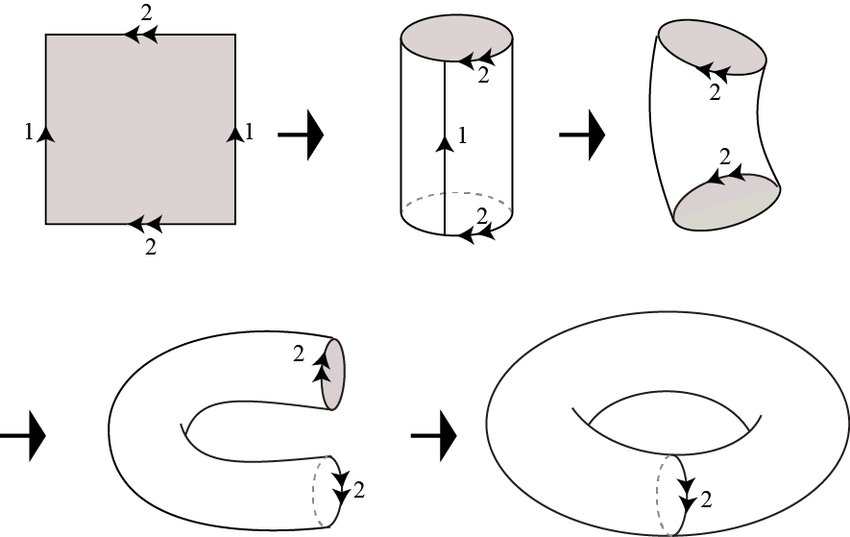
위 그림을 보면 직사각형을 이용해 토러스를 구축할 수 있음을 알 수 있다. 이런 구축 방법을 수학의 언어로 바꾸어 보자.
Def. Let $X$ and $Y$ be topological spaces; let $p : X → Y$ be a surjective map. The map $p$ is said to be a quotient map provided a subset $U$ of $Y$ is open in $Y$ if and only if $p^{-1}(U)$ is open in $X$.
이 조건은 앞에서 정의한 연속함수의 정의보다 강력하다. (strong continuity)
동치조건으로는 다음이 있다.
(1) subset $A$ of $Y$ is closed in $Y$ iff. $p^{-1}(A)$ is closed in $X$. (2) $p$ is continuous and $p$ maps saturated open sets of $X$ to open sets of $Y$.
여기서 saturated set(포화집합)이란 다음과 같다.
Def. Let $p : X → Y$ be a surjective map. A subset $A$ of $X$ is said to be saturated with respect to $p$ if $p^{-1}(p(A)) = A$.
정의에 따라 open, closed map은 quotient map이다.
자, 이제 quotient map을 이용해 몫위상을 정의할 수 있다.
Def. If $X$ is a space and $A$ is a set and if $p : X → A$ is a surjective map, then there exists exactly one topology $\mathscr{T}$ on $A$ relative to which $p$ is a quotient map; it is called the quotient topology induced by $p$.
만약 $A$가 $X$의 partition $ X^* $라고 하자. 그러면 $ p : X \rightarrow X^* $는 surjective map이고, 각 원소가 어느 partition에 속하는지 알려주는 함수가 된다. 이 함수는 quotient space(몫공간)을 유도한다.
Def. In the quotient topology induced by $p$, the space $X^*$ is called a quotient space of $X$.
이 정의는 현대대수학의 몫공간과 대단히 유사하다. 이미 현대대수를 공부해 보았다면 Supplementary Exercise에서 관련 문제를 풀어보도록 하자.
추천 연습문제
- 22장 - Ex. 2, 4, 5, 6
- Supplementary Ex. Topological Groups: 1, 4, 5, 6, (7)
다음 포스트에서는 연결성(connectedness)과 옹골성(compactness)에 대해 알아볼 것이다. 포스트를 읽기 전에 추천 연습문제를 풀고 충분히 배운 내용을 익히도록 하자자.
퀴즈
[O/X Quiz] 어떤 집합의 멱집합은 언제나 위상이다.
힌트 정답확인
[O/X Quiz] 위상공간의 어떤 원소를 기저의 원소들의 교집합으로 표현하는 방법은 유일하다.
힌트 정답확인
[O/X Quiz] Lower Limit Topology($\mathbb{R}_l$)와 K-Topology($\mathbb{R}_K$)는 비교가능(comparable)하다.
힌트 정답확인
참고자료
[1] Munkres, James R.. Topology. 2nd ed.
글쓴이의 부탁
본문 오류발견 신고 혹은 문의는 댓글로 부탁드립니다.
각주
[1]: 여기서 $\mathscr{P}(X)$는 X의 모든 부분집합들의 집합인 멱집합을 말하고, 필기체로 된 $\mathscr{T}$는 Topology의 맨 앞글자 T를 따서 위상이라는 의미를 나타낸다.



댓글남기기